椭圆曲线初学

随手整理的，可能全是错。。

椭圆曲线方程:$y^2=x^3+ax+b$，其中$a,b\in R$

判别式：$\Delta = -16(4a^3+27b^2)\neq0$

当$\Delta>0$时，曲线有两个联通分量，$\Delta<0$时候有一个联通分量。

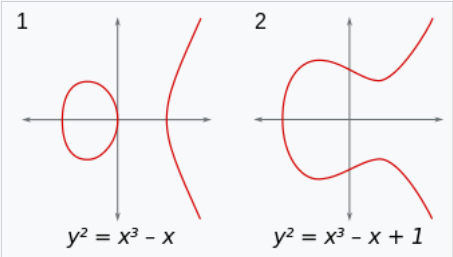
椭圆曲线的运算

定义了一个$E$上的交换群，这个群以无穷远点$O$为单位元。
定义 + 运算子：取E上的两点$P$,$Q$，若两者相异，$P + Q$表示穿过$P$和$Q$的弦和椭圆曲线相交的第三点，再经x轴反射的镜像点；若两者是同一点，$P+P=2P$表示以$P$为切点和椭圆曲线相交的点再经x轴反射的镜像点。若P和Q的弦与y轴平行，$P+Q=0$（无限远点）。
性质1：$O+P=P+O$
性质2：$-P=(x,-y)$
具体运算：要是我上高中沉迷于圆锥曲线肯定是会动手算的，可惜现在早已没了当时的劲头：
$P_3=(x_3,y_3)=P_1+P_2\neq O$ $x_3=k^2-x_1-x_2$ $y_3=k(x_1-x_3)-y_1$ $其中k=\dfrac{y_2-y_1}{x_2-x_1},(x_1\neq x_2)或\dfrac{3x_1^2+a}{2y_1}.(x1=x_2)$

素域上的椭圆曲线

模$P$,除法全变成逆元。

$GF(2^n)$上的椭圆曲线

椭圆曲线上的加解密

用户A的私钥$n_A$,公钥为$P_A=n_A\times G$

用户A的私钥$n_B$,公钥为$P_A=n_B\times G$

A将消息$P_m$加密过程：

选取随机数$k$,密文$C_m=\{kG,P_m+kP_B\}$，简记为$\{C_1,C_2\}$

解密过程：$C_2-n_BC_1=P_m+kP_B-kn_BG=P_m$，解密完成。

椭圆曲线上的密钥交换

用户A的私钥$n_A$,公钥为$P_A=n_A\times G$

用户A的私钥$n_B$,公钥为$P_A=n_B\times G$

A产生的密钥$K=n_A\times P_B$,B产生的密钥为$K=n_B\times P_A$

可以发现$n_A\times P_B = n_A\times n_B\times G = n_B \times P_A$

可以进行密钥交换。

具体应用

求一条椭圆曲线的阶，这个可以用schoof算法在多项式时间内解决。

schoof链接
已知一个点，求这个点的阶，这个用hasse算法也可以解决。

链接
生成标准里要求$n$为素数，那么实际问题都是我们已知$n$,去求$G$。

原以为这些都要自己手动实现，后来经助教确认不用了，那就简单记录一下sage里面椭圆曲线的用法

E = EllipticCurve(GF(p), [a, b]) #表示生成一个参数为a,b,p的椭圆曲线
E.order() #群的阶
E.gen() #生成元
P = E.random_point() #随机一点
P = E(xxxxx,yyyy) #点的坐标
P.order() #元素的阶
P.discrete_log(Q) #P,Q是曲线上两点，尝试去求离散对数

FYHSSGSS's blog

babyECC